A Case Against the Halting Problem (draft)
6 August, 2022
The halting problem is a well known dilemma in Computer Science. It poses a task that is impossible to solve by a computer, regardless of it's speed or capacity, and is often viewed as an important limit on computation.
Here, I argue against that perceived importance. And that, for practically all realistic situations, the halting problem doesn't come into play.
For those who don't know the halting problem, or are unfamiliar with Computer Science, I provide an introduction. But I will be arguing against the theory that I'm introducing, so if you're hoping to learn something new and groundbreaking, you might be disappointed. But if you're curious as to how a well‑regarded theory in computing might not deserve it's status, read on.
An Introduction for Unfamiliar Readers
Skip
Computers, Broadly Speaking
For many, the word 'computer' brings to mind a laptop, desktop, or mobile phone. We can broaden this to include embedded systems (such as the chips in a printer or car) and mechanical systems like Pascal's Calculator.



Source
- Website
- Author: A.Savin
- Date: 2 Jan 2021
- License: Free Art License
Source
- Website
- Author: Johann H. Addicks
- Date: 2008
- License: cc-by-nc-nd 3.0
Source
- Website
- Author: Rama
- License: cc-by-sa 3.0 fr
In Computer Science, we need to talk about computers regardless of whether they consist of transistors, vacuum tubes, or some exotic future technology. So we need a more abstract definition.
There are many possible choices. A general commonality is that computers are objects that autonomously perform actions (like flashing a screen), often in response to instructions or signals (like a button press).
More abstractly, they can accept input data (which can describe instructions) and produce output data (which can trigger actions). The output is determined from the input and the internal state, and is 'computed' from them.

They can be viewed as systems that, given input over time, produce a particular pattern of output over time. That data (possibly in the form of binary ones and zeros) generally encodes some form of information, like a sentence or an image. So computers can be viewed as systems that 'convert' information.
The same view applies to computer programs. A web browser can be seen as a system within a computer, which takes input (like keystrokes and system alerts) and computes output (like sound data and internet messages).

A computer system accepting encoded data from multiple sources, processing them with programs like a web browser and file manager, and sending output to multiple devices.
Extra Fundamentals
Arguably, it is highly‑flexible information conversion, along with simple inputs/outputs, which makes computers so useful.
If someone wants to design an object with some desired behaviour, such as a car, that behaviour generally depends on information from the external world and internal state. A car needs information from the driver, possibly via a steering wheel and buttons. That info, along with it's internals, determine it's behaviour, which is triggered by sending output signals to wheels, headlights, etc.
Without computers, converting inputs to outputs involves laboriously combining converters like gears, levers, wires, and so on. These are limited in what conversions they can make, and in how they combine with each other. A computer provides one general converter for all of this, and can be reprogrammed to adjust that conversion as needed.
With this definition, we can include many things not conventionally viewed as computers. A group of molecules can be viewed as a computer, where the inputs/outputs are chemical interactions (as in nanomachines). A living cell can be viewed as a system of organelles and chemicals, with behaviour determined by sensory information and internal state (such as it's temperature, hunger level, or memories). We could also include insects, humans (debatably), social systems, weather systems, solar systems, and so on.
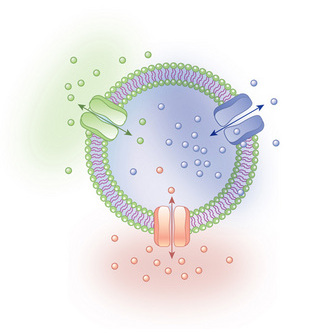
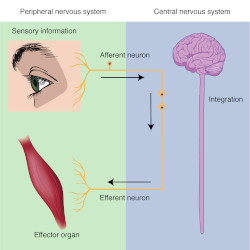
Source
- Website
- Owner: Nature Education
- Date: 2010
- Terms of Use: User Agreement
Source
- Online Book
- Book Title: Anatomy & Physiology
- Authors: Lindsay M. Biga, Sierra Dawson, Amy Harwell, Robin Hopkins, Joel Kaufmann, Mike LeMaster, Philip Matern, Katie Morrison-Graham, Devon Quick, and Jon Runyeon
- License: cc-by-sa 4.0
Source
- Online Book
- Book Title: Life Sciences Grade 10
- Owner: Siyavula Education
- License: cc-by 3.0
The Halting Problem, in Brief
The halting problem uses another definition for a computer, called a Turing machine. These are minimalistic machines that read and write symbols on a tape. Theoretically, any computer can have it's input‑output pattern replicated by a Turing machine. In this way, Turing machines are 'equivalent' to other computers.

Left: A Turing machine with a tape holding input '10'
Right: After running, the tape now holds output '1001'
The halting problem describes a hypothetical Turing machine that can figure out whether any given Turing machine will eventually finish running and produce an output. The theory goes on to say that no such machine exists, because, if one did, it would result in a logical contradiction.
And because Turing machines are 'equivalent' to any real‑life computer, the implication is that there are some apparently straightforward problems, like finding out whether a computer halts, that computers simply cannot solve.
The Halting Problem: A Review
Skip
Turing Machines
A Turing machine can be visualised as a box with a mechanical head that can read and write one symbol on a tape at a time.

Initially, the tape holds an input, and the machine is in some starting state. Repeatedly, the machine will read the symbol under the head, write one symbol, move the tape by one spot, then change state. The decision of what to do is fully determined by what symbol was read and what the current state is.

On the left, the machine reads 1 from the tape, and is in starting state S. The machine then acts according to the table in the middle, which says, for 1 and S, the machine should write 0, move the tape upward, and go to state A.
One state can be a 'halting' state. If the machine enters this, it will finish running, and the contents of the tape are taken as the output. If this state is never entered, the machine simply never halts, and has no defined output.
Click to step through the process
The tape is considered 'infinite', so no matter how many times the tape is moved, there is always more tape to write on. This does make the machine unrealistic, but for the purpose of showing the limits of computation, using something more capable than realistic is acceptable.
Extra Technicalities
In addition, the set of states and symbols must be finite.
Alternative definitions exist. They might allow multiple halting states, optional tape movement, or multiple tapes. But in each case, the input‑output capability remains the same.
Here's a more complex example. For input, it expects two binary sequences, separated by a special symbol. The output is the second sequence, in reverse, followed by the first sequence. For instance, the inputs '11' and '10' would produce '0111'.
Click to animate the computation
Turing Machines as Input
Turing machines themselves can be encoded as input. The 'decision tables' shown above can be written onto a tape row‑by‑row, with row‑separator symbols. Any extra data (like a list of multiple halting states) can be similarly added, as regions of symbols with separating markers.
Computational Equivalence
Most modern computers, at their core, consist of memory that holds files and code, a processor that fetches code from memory and executes it, and circuitry that connects them up with other components, such as a USB port or cooling fan.

Input components (yellow) and memory (green) send data to the processor (blue), which sends data to memory and to output components (red)
It's possible to build Turing machines that mimic the cycle of fetching and executing code. The tape can hold memory, and encode input and output to other components. In this way, a Turing machine can replicate a modern computer.

Turing Completeness
Systems that can simulate any computer (or Turing machine) are called 'Turing complete'. The term has been used for machines, software, math constructs, and more loosely for languages, games, and the human mind.
It can be surprising how little complexity is needed for a system to become Turing complete. Aside from Turing machines, other examples include cellular automata, logic gates, and certain very minimal programming languages. There are also many cases of accidental Turing completeness.
The Halting Problem
The halting problem poses the task of making a Turing machine X that can determine, in general, whether some input Turing machine will halt on some input.
More specifically, X's input will describe a Turing machine T and an input I for it, and X's output will be a Yes or No symbol, indicating whether T will halt on I. X must always halt and give a correct answer.

To avoid a common source of confusion, X must do this in general. It can't be right for only some cases. It needs to be right for all cases. And there is a proof that this is impossible.
Proofs by Contradiction
This form of proof aims to prove a statement S using an argument like "If S was false, this would result in a logical contradiction, so S must be true".
As a detailed example, let's say we wanted to prove "1 is not less than 1". And let's assume that our system of reasoning is very limited, and that this statement is not obvious to us.
- We would first consider what would happen if the statement was false. The opposite statement "1 is less than 1" would be true.
- Let's say our limited reasoning knows we can convert statements like "X is less than Y" into "Y is larger than X", without changing the truth of the statement. So we could deduce that "1 is larger than 1".
- And let's say we also know that being larger than something implies not being less than it. So we could deduce that "1 is not less than 1".
- So, from "1 is less than 1", we could deduce that "1 is not less than 1", which is a contradiction, saying that something is both true and false.
- We could then conclude that "1 is less than 1" cannot be true, so the original statement "1 is not less than 1" must be true.
Here, we're using a mathematical definition of 'logical contradiction', where a statement is both true and false. For the more everyday meaning of something 'not making logical sense' (eg. "I am tall and short"), things are different. The contradiction might be due to incomplete information (eg. "Tall and short from different perspectives) or a misconceptualisation, and might not imply falsehood.
Let's suppose X does exist. It could then be used to construct another machine Y.
Y takes an encoded machine Z as input, then copies X's behaviour, using Z as both inputs. If the output is Yes, Y proceeds to loop indefinitely, forever jumping between non-halting states. If No, Y halts and outputs something.

Y uses X to determine whether Z halts with input Z, then does the opposite of what X says Z would do
If we run Y with an encoded Y as input, we come across a logical contradiction.
- If the inner X outputs Yes, Y will loop indefinitely, which is a problem, because we've just run Y with Y as input, and X said Y would halt.
- Similarly, if the inner X outputs No, Y will halt, in contrast to what the inner X said it would do.
So, if X did exist, we could make a machine that shows X to be wrong. The implication is that X cannot exist, and no Turing machine can solve the halting problem.
Related Problems
Because Turing machines can replicate other computers, this implies that no computer can solve the halting problem. This leads to another question. How many such problems are there?
It turns out there are many problems where, if they had a solution, it could be used to solve the halting problem. We say the halting problem can be 'reduced' to those problems.
Such problems generally have the form 'determine whether a Turing machine T satisfies property P', where P is a 'non trivial property'. Examples include figuring out whether a Turing machine will halt on any input, or even just whether it outputs Yes for a particular input.
But, if the halting problem is unsolvable, then surely solutions to these problems can't exist. The conclusion is that using computers to figure out anything 'non trivial' about other computers, in general, is impossible. This is summed up in Rice's Theorem.
Reduction Example
(Warning: Lots of variables ahead)
As an example, consider the problem of determining if a Turing machine outputs Yes for input '0'. Let's assume we have a machine X that solved this problem, outputting Yes or No for an input machine Y.

We could construct another machine Z that takes a Turing machine U and an input I. Z uses U and I to write out a machine V, then runs X with V as input, and outputs the result. V is a machine that ignores it's input and runs U on I.

Z uses U and I to write out a machine which will be analysed by X
As it turns out, Z would solve the halting problem.
- If U would halt on I, V will halt regardless of it's input, and would halt on '0'. So X outputs Yes, and Z outputs Yes.
- If U would not halt on I, V never halts, and would not halt on '0'. So X outputs No, and Z outputs No.
And so, because X could be used to solve to the halting problem, we say that the halting problem is reducible to this problem.
Consequences
This result is somewhat disappointing. There are many properties about computers that would be useful to obtain automatically. Knowing whether a program will halt or crash, ahead of time, would be very helpful. It could be used to reduce errors, find security holes, and shortcut many algorithms, making programs run faster.
A solution could also be used to solve mathematical problems like the Collatz conjecture, Goldbach's conjecture, and the Riemann hypothesis. The last is one of the Millenium Prize problems, for which solutions have a reward of one million dollars.
Hypothetical Solutions
The above math problems can be rephrased into 'Does there exist an X with property P?', where the number of Xs is infinite. We could write a program that searches through Xs forever, only halting if it finds one that satisfies P. If we knew whether such a program would halt, we'd have an answer to the question.
An Alternate View
A common counterpoint to the above is that, even though we can't solve the halting problem for all cases, perhaps we could still solve many of them. But it's unclear where that threshold lies. Rice's theorem seems to imply that almost all 'interesting' cases are beyond us.
The Finite Case
To start off, let's consider Turing machines that don't need an infinite tape. They only need a tape with N symbols, where N might be a hundred, or a thousand, or higher, but is some fixed number.
For these machines, it's actually quite straightforward (if inefficient) to determine whether they halt. Because they use a finite amount of tape, and have a finite set of states, there are only so many situations of state, tape contents, and head position that are possible. You can simply run the machine, and note down what situations it's been in. If the machine never halts, it must eventually enter the same situation twice, and you can detect this and output No. And if it does halt, simply output Yes.
This operation can be done by a finite‑tape Turing machine, although it will likely use a lot more tape than the machines it analyzes (to hold all that noted‑down information). And it won't be able to handle cases above a certain memory limit.
We still don't have a single machine that solves all cases. But we can construct many machines, each able to solve for cases under a certain limit. In reality, we could even build a machine that extends itself with memory, moving it's limit upward as needed. This is arguably enough.
As an analogy, consider a rope maker. If they were tasked to make a rope longer than all possible ropes, that's a problem, because whatever rope they build, it won't be longer than itself. But that doesn't seem to matter in reality, because being able to make a rope longer than any particular length is good enough. And viewing it as a 'rope‑making problem' doesn't seem appropriate.

Multiple Turing machines, each with a set of cases it can solve. And multiple ropes, each with a set of shorter ropes.
Going Deeper
But what if there is some obscure situation where we need a machine that solves all cases?
Well, if you're allowed to use an infinite‑tape machine, you can do this. There is no limit to the number of situations you can note down, so you'll eventually spot a halt or a cycle.
But let's say infinite tapes aren't possible. That would imply that the universe is finite, which limits the set of machines that we could actually build. So if we're only analyzing machines that are real, we wouldn't actually need to cover all cases.
The Infinite Case
Now let's consider infinite tapes. If we found a source of infinite memory in real life and could make them, how would the halting problem affect us?
If we could turn infinite‑tape machines into finite‑tape versions, the finite case above would apply. You might notice that, while a Turing machine is running, at any one point in time, the used part of the tape is finite. So if the machine halts, it only ever needed a finite tape. And if it doesn't halt, it's behaviour could be replaced by one that doesn't use the tape, and simply loops forever.
So, for any given machine, we might get away with a finite tape that is sufficient for the largest case. Unfortunately, this doesn't always work. If there are infinitely many cases, and for each one there is another that needs more tape, there won't actually be a largest case.
Another argument questions whether knowledge of the halting problem would really change our decisions. The halting problem says we can't build a machine that solves all cases, but it doesn't stop us building one that solves particular cases. And whenever we're faced with analyzing a machine we haven't seen before, the choice of whether to try or not remains present, even with the halting problem, because there might be a solution for this particular case.
But let's say we specifically want a machine that handles all cases. Maybe infinite‑tape Turing machines are very expensive to make, and to reprogram, so we can't tailor them to particular cases.
That hypothetical machine might not be as useful as expected. When a solver for the halting problem says that a machine will halt, that machine might still take a very long time to do so. Furthermore, the solver itself might take a long time to tell us. And aside from the inconvenience of waiting, running a computation for a finite (but indefinite) time, without interruption, is no small task. Real‑world issues like power outages, natural disasters, civilisation collapse, and so on, are all obstacles to ensuring a finite‑time computation succeeds.
One could argue that having such a solver would still be helpful in the shorter term, as it would sometimes finish quickly. But that's not really better than a non‑general solver, which also only sometimes gives a result. And because the halting problem permits the latter, it arguably doesn't make much difference.
Going Deeper (Highly Speculative)
But what if we could ensure that those finite‑time computations succeed, regardless of how long they take?
Firstly, if you accept the broad definition of 'computer' above, the ability to ensure a computation succeeds could actually be used to preserve a system indefinitely. It could be used for eternal storage, immortality, and avoiding the end of the universe. But let's ignore that, and just consider cases relevant for the halting problem.
The issues from above still apply, so someone who starts such a computation would need to accept the possibility of it taking a very long time. To ensure the computation is worthwhile, the result would need to matter to them even after billions of years. What would such a computation look like?
For the computation to matter, it's result must trigger some action. And if that action needs to matter long after the lifetime of the creator, it arguably needs to be selfless, independent of any particular person. Maybe the computation predicts the final state of the universe, and in the case of a big rip or heat death scenario, the action is to trigger a new big bang.
There also needs to be an alternate action, taken upon a different result. Otherwise we could just do the action unconditionally. Maybe we want to avoid triggering a big bang if the universe is cyclical (and naturally cycles between big bangs and big crunches), perhaps because the manual way is less reliable.
And let's say we want to know if such a computation halts. So if the computation fails to predict the universe, maybe we want to trigger a big bang anyway, just in case. Perhaps in this scenario, the halting problem would save us from attempting this, by saying it is impossible.
Or perhaps not. Given the constraints above, the set of computations 'worth taking' seems quite narrow, so the general solution denied by the halting problem is probably not needed. But for the sake of speculation, let's say the set is diverse enough that we want a general solution anyway.
As a last‑ditch argument, perhaps even then, such a computation wouldn't be wanted. The one starting the computation might reasonably question whether their knowledge and morals will actually remain appropriate by the time the computation ends. If they get it wrong, the mistake would be permanent, because the computation is ensured to complete. A more adaptive computation might be more appropriate. Maybe a societal one, which involves doing what computation you can, then passing that knowledge on, leaving the (hopefully wiser) future to decide whether the task is worth continuing.
Consequences
To summarise, for the finite case, even though we can't build a single general solution, we can build one for any particular case. And for any realistic purpose, this is arguably enough.
And for the infinite case, it only becomes relevant in real life if we find a source of infinite memory. And if we do, we might be able to convert the machines to finite‑tape versions. And if we can't, the halting problem doesn't prevent a solution for particular machines. And even if we needed a general solution, we'd run into issues with long‑term computation before the halting problem stops us.
Based on the above, it is my view that, for almost any practical (and realistic) purpose, the unsolvability of the halting problem isn't really important.
It's easy to view the halting problem as saying that the task of generally analyzing programs is impossible. And while that may be true in a certain restrictive sense, the way it's commonly interpreted can be misleading. The 'generally' part arguably restricts the statement so much that it's not worth saying.
And, while the halting problem does play a role in computing theory, perhaps it shouldn't have the 'core' role that it's often considered to have. I've yet to find a significant real‑life consequence from theories derived from it, and it's role in pure theory seems similarly restricted by the points above. It might have even over‑discouraged work in computational analysis, due to being interpreted too strongly.
There is a field of computing called termination analysis, which tries to recognise halting in practical scenarios. It appears fairly obscure, with relatively few people working on it. There's a certain feeling that the field could never be complete, due to the halting problem. But, as outlined above, perhaps completeness is far less important than it appears.
Final Thoughts
When I first learned about the halting problem, it took a while to understand and accept, and I thought the consequences were profound. But when I tried to explain it, there was often a feeling of unease, like I was missing part of the picture. And I suspect this is not uncommon.
That unease persisted over several years, until I'd gathered a loose handful of counter‑ideas. Some of them are well known. For instance, finite‑tape Turing machines are also called linear bounded automata, for which the halting problem is known not to apply. But I was unable to find them in a collected form, and thought structuring them into one document would be helpful.
Having finished, I'm conflicted. I'm fairly confident that I'm right, which puts my mind at ease. But even then, all it does is avoid a limitation that we weren't really running into. The task of analyzing programs is still hard, even if it isn't really impossible. But for me, it does add hope that we might actually find efficient practical solutions someday. And if not, it was at least helpful to correct a past misapplication of theory to real life.